Introduction

To aid with the development of StudioViz, a simulator created by Cepton’s in-house software engineers, I worked to create a script that generates Ground Height Grid for Wavefront OBJ files.

When developing a game engine, knowing the height of the ground level is crucial. It helps to ensure that object models, such as cars and pedestrians, actually stick to the ground. Take the following picture for example:

Within this picture, two distinct ground heights are important. The first one is the height of the road. This is the only height that cars are allowed on. The second one is the height of the sidewalk, which is slightly elevated relative to the road. Cars are not allowed on the sidewalk. Pedestrians, however, can freely move between the sidewalk and the road. They will need to be programmed to adjust to the new difference in height when walking from one to the other. There are other considerations as well. For example, think about walking under a street light.

The game engine will need to be able to recognize that the street light is there and that cars and pedestrians can walk underneath it. These are all eventual goals of implementing a ground height feature into StudioViz, and the creation of a ground height gridmaker helps with crucial preprocessing of the models so that the simulator’s game engine does not need to make these calculations in real-time.

Basic Explanation of OBJ files

Wavefront OBJ files are a standard 3D image format used to represent 3D geometry. Each obj file contains the positions of vertices and faces. More on that later, here is an OBJ file of a cube:

In the context of OBJ files though, ‘faces’ are often defined to be a triangle of three vertices. So for our earlier example, 12 different faces are comprised to create the cube, with two faces being paired together to create the image of a flat square on each of its sides.

With only the data of vertices and faces, you can create incredibly complex object models! Using enough triangles will also give off the illusion of a round object. Here is an object model of a tire, that uses many faces to give it its round appearance.

Below is the obj file that we eventually want to work on. It is a city model, with a total of 405,163 vertices and 673,096 faces:

Creating and Optimizing a Ground Height Grid

The grid we want to make spans across the xy-plane of the OBJ file. It takes the centerpoint of each square cell and evaluates the highest z-value at that coordinate. The idea is that by using small enough squares for the grid, we can get detailed ground-height data across the OBJ file. The cleanest, most systematic approach to generating this grid is also extremely inefficient, with it being O(n^2). The approach is this:

For every single face in the entire OBJ file, calculate if it intersects with the centerpoint of a square cell. If it does, then calculate the z-value of the intersection and eventually through iterating through all the faces, you will find the highest z-value. Then repeat that whole process for every new square cell you want to make until the whole grid is generated. Here are optimizations we can make are all about reducing the number of faces needed to parse through.

Optimization #1: Remove all vertical faces

Here is what the city model looks like with all vertical faces removed:

Usually this is not enough on its own, but it does significantly reduce many of the faces.

Optimization #2: Ignore faces above a certain z-value

If we are only looking at the ground, then we can delete all the vertices and faces above a certain y-level, as the buildings take up a lot of faces. Here is the city model when removing all vertices and faces above three meters. As you can see, it basically takes out all the buildings:

Algorithm

Here is the actual raw algorithm for finding the highest z-value of an individual cell.

def cell_value(self, center: tuple, sq_vertices: list) -> float:
        """
        Calculates the highest z-value of each cell.
 
        First, this method creates a list of all the faces that intersects the
        square cell itself. This is probably the most inefficient part of the
        process. Then, it calculates all the intersections of those faces that
        the center of the square has. Then it returns the highest intersection,
        or None if there were no intersections.
 
        Args:
            center (tuple): The center coordinate of the square cell.
            sq_vertices (list): The vertices of the square cell.
 
        Returns:
            float or None: The highest intersection at the center of the cell.
        """
        curated_faces = self.faces_in_square(sq_vertices)
 
        def intersections_at_center(center: tuple, faces: list):
            z_values = []
            for face_index in faces:
                face = self.faces[face_index]
               
                v0 = self.vertices[face[0]] # vertex 0's 3D coordinates
                v1 = self.vertices[face[1]] # vertex 1's 3D coordinates
                v2 = self.vertices[face[2]] # vertex 2's 3D coordinates
                triangle = [(v0[0], v0[1]), (v1[0], v1[1]), (v2[0], v2[1])]
                # 2D triangle created by projecting the 3D triangle onto xy-plane
 
                if self.is_point_in_2D_triangle(center, triangle):
                    triangle_3D = [v0, v1, v2]
                    z_values.append(self.find_z_value_on_plane(center, triangle_3D))
           
            return z_values
       
       
        intersects = intersections_at_center(center, curated_faces)
        if len(intersects) == 0:
            return None
        return np.max(intersects)

It first starts by curating a list of all the faces that intersect with the square cell. This is probably the most computationally heavy portion of the algorithm, as it iterates through all of the faces. However, the calculation for determining if a triangle and square intersect is relatively simple. It uses the Separating Axis Theorem (which is covered more in the previous blog post about Collision Detection). After creating a more curated list of triangles, the algorithm determines if the center of the point is inside a triangle and proceeds to calculate the z-value of its intersection. Using a simple grid managing algorithm, These centers and values can be put into a dictionary for easy look-up.

def grid_maker(self, square_size: float) -> None:
        """
        Generates the Ground Height Grid
        """
        self.grid_values_init()
        self.square_size = square_size
        self.grid_size = self.precalculate_grid_size(square_size)
 
        index = 0
        x = self.x_min
        while x < self.x_max:
            y = self.y_min
            while y < self.y_max:
                center = (x + self.square_size/2.0, y + self.square_size/2.0)
                bottom_left = np.array((x, y))
                bottom_right = np.array((x + self.square_size, y))
                top_right = np.array((x + self.square_size, y + self.square_size))
                top_left = np.array((x, y + self.square_size))
                sq_vertices = [bottom_left, bottom_right, top_right, top_left]
 
                z_value = self.cell_value(center, sq_vertices)
                self.grid[center] = z_value
 
                index += 1
                print('Progress Bar:')
                print(str(float(index/self.grid_size) * 100) + '%')
 
                y += self.square_size
            x += self.square_size

Visualization

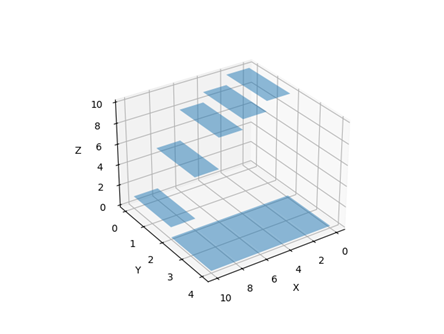
Here is a test case that contains different height levels.

Here is a visualization of what running the grid_maker will generate. It takes the value of each cell and recreates the square at its respective z-value:

Conclusion

Creating a Ground Height grid is very important for the development of game engines and simulators. The most straightforward approach, however, is often the most computationally heavy. Intelligent optimization and ways to reduce the number of objects needed to parse through are necessary for computing this essential precomputation.